MODELLING CONCEPTS
N-Poles and Termination.
Any vertex which has 3 edges emanating from it is called an n-pole. The quad spehere below has the N-Pole highlighted in white.
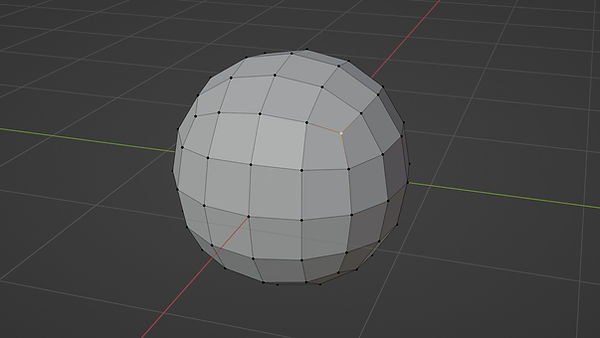
A Quick Way to remember which of the poles is an N-pole is to visualise the letter N created with Matchsticks. You would need 3 matchsticks to make the capital letter "N".
You will find them everywhere in almost every 3d model. In polygonal modelling you will commonly find them on corners. It seems like the natural place to have an n-pole but in subdivision surface modelling we try to avoid having them on corners. When they do appear we try to move them to areas of minimal distortion or the pinching effects they create will be seen in renders.
N-poles occur because a change of directing in your topology has occurred and they can normally be moved - with an inset - to within one or ideally two loops distance - from an edge or corner. This is the area of a local geometry which is the least likely to undergo distortion during animation or deformation.
In the following example the cube on the left has N-poles on it's corners. This is undesirable as the light will be pinched slightly making the corners seem sharper than they would in real life. It is a minor concern and they are often left this way but for very precise modelling the corners should be corrected by insetting the top face. We call this termination. The cube on the right has four spoked poles on the corners. It has been correctly terminated.
N-Poles are vertices with 3 edges emanating from them

Un-terminated face vs terminated face.
A quadsphere is a classic example of the problems created by N-poles and the section where we recreate the sphere as a subdivision surface model demonstrates this.
The unwanted effects of an N-Pole can also be negated, or a least minimised with the use of the "Smooth Laplacian" modifier. An example of its usage can be found in the Boolean sphere section of this website.